[알고리즘]다익스트라 알고리즘

다익스트라 알고리즘은 최단 경로를 알기위한 알고리즘입니다.

즉 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려줍니다.

그러나 해당 알고리즘은 음의 간선을 포함할 수 없으므로 이를 유의해야 합니다.

 

또한 이를 구현하는 방법에 힙 자료구조를 이용하는 방법이 있어,

자바를 이용해 구현하는 본 게시글에서는 PriortyQueue 클래스를 활용하여 구현하는 코드를 포함합니다.

 

다음은 예제입니다.

(그림 1) 예제에 사용될 그래프

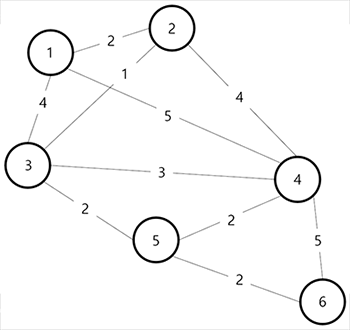
다익스트라의 진행 순서는 다음과 같습니다.

1. 시작점을 선택

2. 이동이 가능한 노드 중 가장 거리가 짧은 노드를 선택

3. 현재 구해진 각 노드까지의 거리와 선택된 노드를 거쳐 각 노드를 방문하는 거리를 비교
-> 선택된 노드를 거쳐 해당 노드를 방문하는 거리가 더 짧은 경우 거리를 갱신

4. 2번과 3번을 목표 지점 노드까지의 거리가 구해질 때 까지 반복

(그림 2)코드의 진행에 따라 선택된 노드와, distance 배열의 변화

CODE

PriortyQueue를 사용하지 않은 다익스트라 알고리즘

import java.util.Arrays;

//PQ사용 안한 다익스트라
public class Diikstra {
	static final int infinite = Integer.MAX_VALUE - 100000;
	static int n = 6;
	static int[] distance;
	static boolean[] isNotVisited;
	static int[][] load = { 
			{ 0, 2, 4, 5, infinite, infinite }, 
			{ 2, 0, 1, 4, infinite, infinite },
			{ 4, 1, 0, 3, 2, infinite }, 
			{ 5, 4, 3, 0, 2, 5 }, 
			{ infinite, infinite, 2, 2, 0, 2 },
			{ infinite, infinite, infinite, 5, 2, 0 }
	};

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		distance = new int[n];
		isNotVisited = new boolean[n];
		Arrays.fill(isNotVisited, true);
		
		diikstra(0,5);
		
		System.out.println("distance");
		for(int i=0; i<n; i++)
			System.out.println("["+i+"] : " + distance[i]);
	}
	
	public static void diikstra(int start, int end) {
		int i, j, now = 0, min;
		
		isNotVisited[start] = false;
		
		for(i=0; i<n; i++)
			distance[i] = load[start][i];
		
		while(isNotVisited[end]) {
			min = Integer.MAX_VALUE;
			
			//방문한 적이 없으며, 가장 거리가 짧은 노드 구하기
			for(i=0; i<n; i++) {
				if(isNotVisited[i] && min > distance[i]) {
					min = distance[i];
					now = i;
				}
			}
			
			isNotVisited[now] = false;
			
			//현재 선택된 노드를 거쳐가는 경우가 현재 거리보다 짧은 경우 교체 
			for(i=0; i<n; i++) {
				if(distance[i] > distance[now] + load[now][i])
					distance[i] = distance[now] + load[now][i];
			}
		}
		
	}
}

PriortyQueue를 사용한 다익스트라 알고리즘

import java.util.Arrays;
import java.util.PriorityQueue;
class Trunk implements Comparable<Trunk>{
	int goal, length;

	public Trunk(int goal, int length) {
		super();
		this.goal = goal;
		this.length = length;
	}

	@Override
	public int compareTo(Trunk o) {
		// TODO Auto-generated method stub
		return this.length - o.length;
	}
}
//PQ사용 안한 다익스트라
public class DiikstraPQ {
	static final int infinite = Integer.MAX_VALUE/10;
	static int n = 6;
	static int[] distance;
	static boolean[] isNotVisited;
	static PriorityQueue<Trunk> trunkQueue = new PriorityQueue<>();
	static int[][] load = { 
			{ 0, 2, 4, 5, infinite, infinite }, 
			{ 2, 0, 1, 4, infinite, infinite },
			{ 4, 1, 0, 3, 2, infinite }, 
			{ 5, 4, 3, 0, 2, 5 }, 
			{ infinite, infinite, 2, 2, 0, 2 },
			{ infinite, infinite, infinite, 5, 2, 0 }
	};

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		distance = new int[n];
		isNotVisited = new boolean[n];
		Arrays.fill(isNotVisited, true);
		
		diikstraPQ(0,5);
		
		System.out.println("distance");
		for(int i=0; i<n; i++)
			System.out.println("["+i+"] : " + distance[i]);
	}
	
	public static void diikstraPQ(int start, int end) {
		int i, j, now, length;
		Trunk nowTrunk;
		
		trunkQueue.add(new Trunk(0, 0));
		
		Arrays.fill(distance, infinite);
		distance[start] = 0;
		
		while(isNotVisited[end]) {
			//거리가 가장 짧은 간선 꺼내기
			nowTrunk = trunkQueue.remove();
			now = nowTrunk.goal;
			length = nowTrunk.length;
			
			//만일 방문한 적 있는 간선이라면 다음 간선 탐색
			if(!isNotVisited[now])
				continue;
			
			//방문 유무 체크
			isNotVisited[now] = false;
			
			//현재 선택된 노드를 거쳐가는 경우가 현재 거리보다 짧은 경우 교체 
			for(i=0; i<n; i++) {
				if(distance[i] > distance[now] + load[now][i]) {
					distance[i] = distance[now] + load[now][i];
					trunkQueue.add(new Trunk(i, distance[i]));
				}
			}
		}
		
	}
}